MNIST For ML Beginnersの和訳
2016年06月28日
Tensorflowのチュートリアルともいえる「MNIST For ML Beginners」の英文について、機械学習初心者ということでまず文章を和訳してみました。
このチュートリアルは、機械学習とTensorFlowの初心者向けの内容となっています。
もしあなたがMNISTが何かを知っていて、多次元ロジスティック回帰(ソフトマックス回帰)が何かを知っているのであれば、こちらの上級者向けのチュートリアルのほうがよいでしょう。
どちらのチュートリアルにしても、事前にTensor Flowをインストールしておいてください。
プログラムについて勉強するときには、まず最初に「Hello World」を出力する伝統があります。
機械学習ではMNISTがHello Worldに相当します。
MNISTはシンプルなコンピュータのためのデータセットです。
それは、以下のような手書き文字で構成されています。
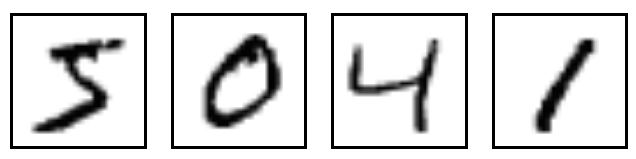
また、この文字セットはそれぞれの画像に対して、その文字が何であるかを示すラベルを含んでいます。
例えば、上記の画像に対してのラベルは5,0,4,1です。
このチュートリアルでは、モデルを文字が何であるかを予測できるように訓練します。
目的としては、最先端のパフォーマンスを達成する精巧なモデルを訓練することではなく(あとでコードを提供します)が、TensorFlowを試してみることです。
そのようなものとして、とても単純なモデルで多次元ロジスティック回帰(ソフトマックス回帰)と呼ばれています。
このチュートリアルで使用するコードはとても短く、たった三行で興味深いことがおきます。
しかしながら、背景にあるとても重要なアイデア(TensorFlowがどうやって動作しているかと、機械学習の中核となるコンセプト)を理解することが重要です。
このため、コードに対して注意深く理解していきましょう。
MNISTのデータ
MNISTのデータは、Yann LeCun氏のウェブサイトにホストされています。
簡単にするため、自動的にダウンロードとインストールするいくつかのpythonのコードを踏んでいます。
このコードをダウンロードして以下のようにインポートするか、以下のように単純にコピー&ペーストします。
from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets(“MNIST_data/”, one_hot=True)
ダウンロードデータは3つのパートに分かれています。
55,000の訓練用のデータ(mnist.train)、10,000のテストデータ(mnist.test)、そして5000の正規化データ(mnist.validation)です。
この区分はとても重要で、それは機械学習に必要不可欠なものです。
最初にも述べたように、MNISTデータは2つに分かれています。
手書きの文字と対応するラベルです。
この画像を「xs」「ys」と呼び、訓練用のデータセットとテスト用のデータセットの両方に含んでいます。
例として、訓練用の画像を「mnist.train.images」、訓練用のデータのラベルを「mnist.train.labels」とします。
それぞれの画像は28×28ピクセルです。
私たちはこれを大きな数値の配列と解釈します。
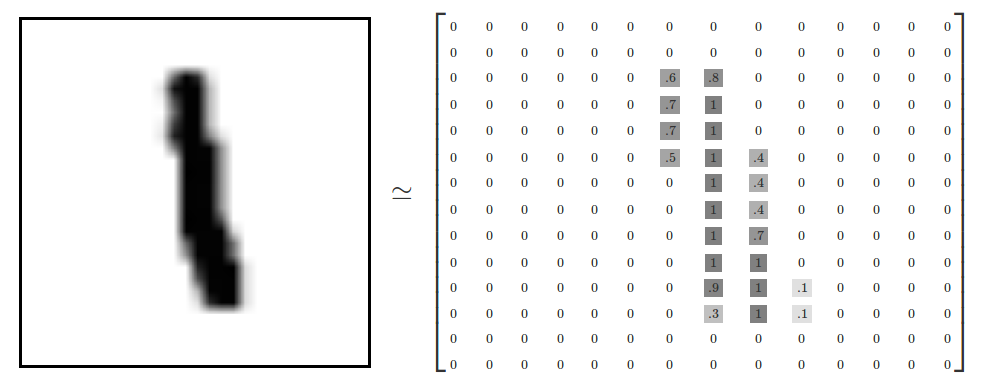
この配列を、線形の28×28=784の数値に戻します。
配列を数値に戻しているのは、画像と一致している限り問題ではありません。
この観点により、MNISTの画像は、とても豊富な構造体(注意:計算的に徹底的な視覚化)付きの、ただの784次元の線形空間です。
データを2Dの画像の構造の情報に戻すことは良くないことでしょうか?
コンピュータがこの構造を利用するとき最適の方法で、チュートリアルの後半でも使用します。
しかしここで使うシンプルな方法がソフトマックス回帰かというと違います。
mnist.train.imagesの結果は、[55000,784]のテンソル(n次元配列)です。
最初の画像の次元のインデックスと、2つ目のそれぞれの画像ピクセルの次元のインデックスです。
それぞれのテンソルのエントリーは、0と1の間であり、特定の画像の特定のピクセルです。

MNISTのラベルは0〜9までで、どの数字がどの画像かを描いています。
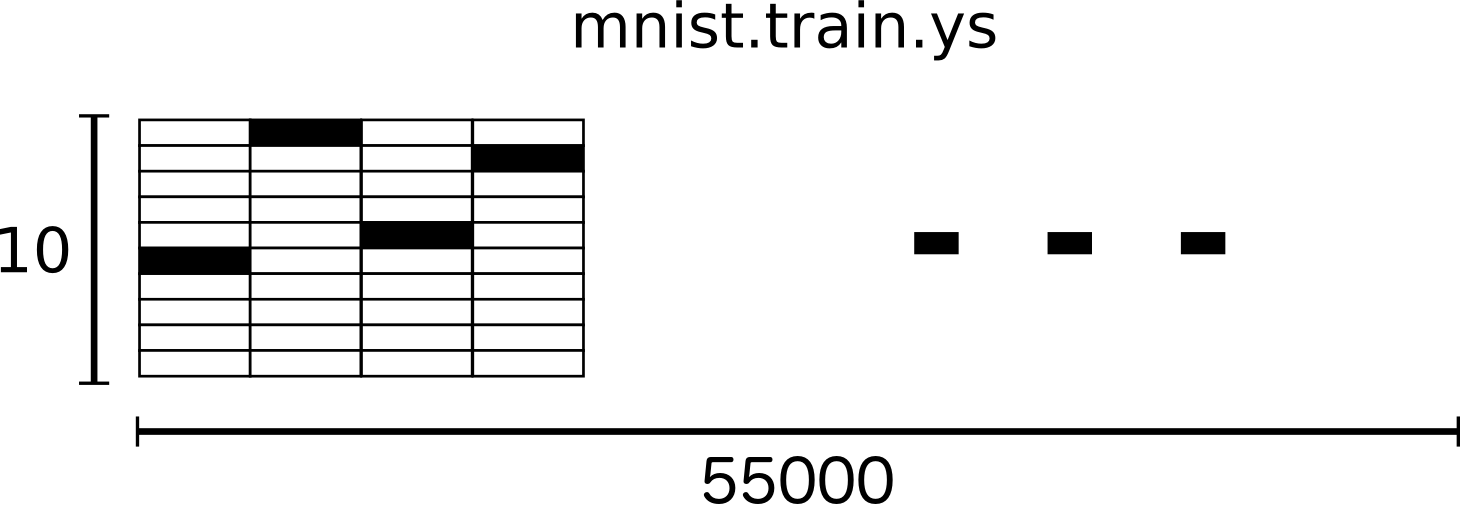
このチュートリアルの目的では、ラベルを「one-hotベクトル」とみなしています。
on-hotベクトルは、多くの次元で0ですが、1は1つの次元であります。
このケースで、n番目の数字が、n番目の次元で1であるベクトルであると表します。
例えば、3は[0,0,0,1,0,0,0,0,0,0]です。
結果的に、mnist.train.labelsは[55000, 10] の配列となっています。
これで、現実的なモデルを作る準備ができました。
ソフトマックス回帰
私たちは、MINSTの全ての画像が0〜9までの数字であることを知っています。
私たちは、画像を見てそれぞれの数字に確率を与えることができるようにしたいです。
例えば、私達のモデルは9の画像を見て80%で9だとします、しかし5%の確率で8になり、少ない確率で他のものになります。
これは古典的なケースで、ソフトマックス回帰が自然で、シンンプルなモデルの場合です。
もしあなたが複数の異なるもの確率を計算したいとき、ソフトマックスでできるでしょう。
後で、より宣伝されたモデルを訓練するとき、最終的にソフトマックスの階層になるでしょう。
ソフトマックス回帰は2つのステップです。最初に正しいクラスの入力のエビデンスを加えて、エビデンスを確率に変換します。
特定のクラスの画像から与えられたエビデンスの計算をすることで、いくつかのピクセルの強度の重みつけをします。
ピクセルがそのクラスにおける高い強度を持ったエビデンスを持っている場合、重みは負になり、エビデンスがin favorのとき正になります。
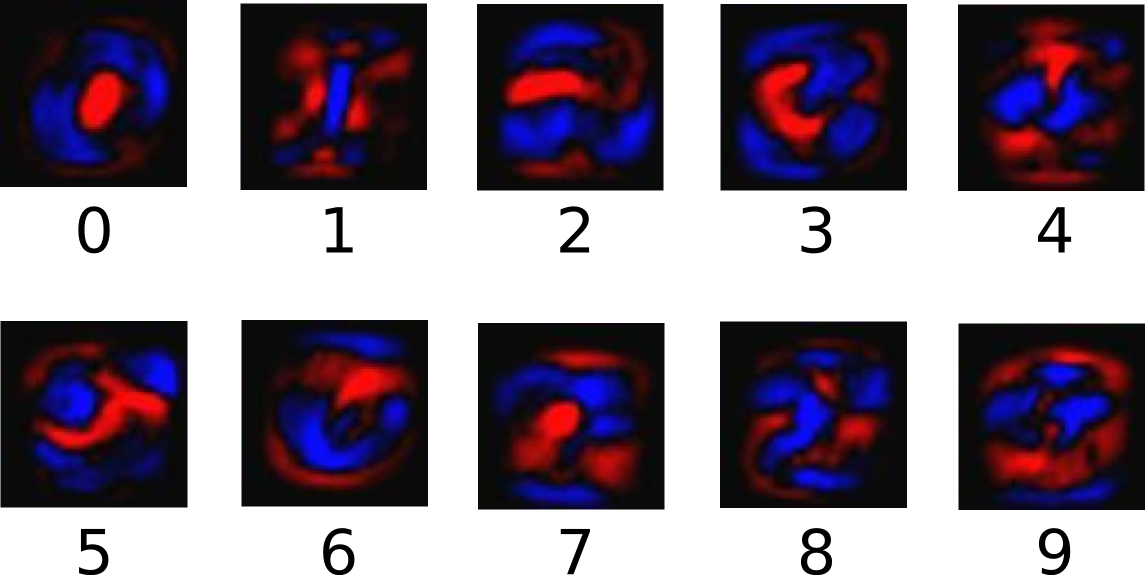
下記のダイアグラムは1つのモデルの重みがそれぞれのクラスを学習していることを表しています。
赤色は負の重みを表していて、青色は正の重みを表しています。
私たちはバイアスと呼ばれる追加のエビデンスを加えました。
基本的に、いくつかの事象は入力の独立にむしろ近いということができます。
クラスiのエビデンスの結果はxを与えます。
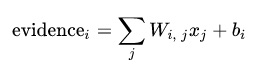
Wiは重みでbiはクラスiとjのバイアスで、入力した画像xのピクセルの総和になっています。
そこでエビデンスの計算を予測された確率に変換します。
yはソフトマックス関数を使用します。
y=softmax(evidence)
ここでのソフトマックスは「起動」か「リンク」関数で、出力された線形関数を必要な形に整形します。
このケースでは、10のケースの確率分布です。
あなたはそれを、エビデンスの計算をそれぞれの入力したクラスの確率に変換することを考えることができます。
それは以下のように定義できます。
softmax(x) = normalize(exp(x))
もしあなたが方程式を展開するのであれば、以下のようになります。
softmax(x)i = exp(xi) / ∑jexp(xj)
しかし、それはしばしばソフトマックスを考えるのにより役立つ第一の方法です。
入力のべき乗と正規化です。
べき乗は、1つ多くのエビデンスのユニットが、いくつかの仮説を倍にする重みを増加することを意味しています。
逆に言えば、1つ少ないエビデンスのユニットは、その前の重みの断片を得る仮説を意味しています。
ゼロまたはマイナスの重みを持つ仮定はありません。
ソフトマックスはこれらの重みを正規化し、そのためそれらは正しい確率分布に加えます。
(よりソフトマックス関数の直感を得ようとするなら、インタラクティブでビジュアルが充実したマイケル・ニールセンの本の章をチェックしてみてください。)
あなたはソフトマックス回帰を、Xsが多いですが以下のように書くことができます。
それぞれの出力に対して、xsの重み付けされた合計を計算し、ソフトマックスに適用します。
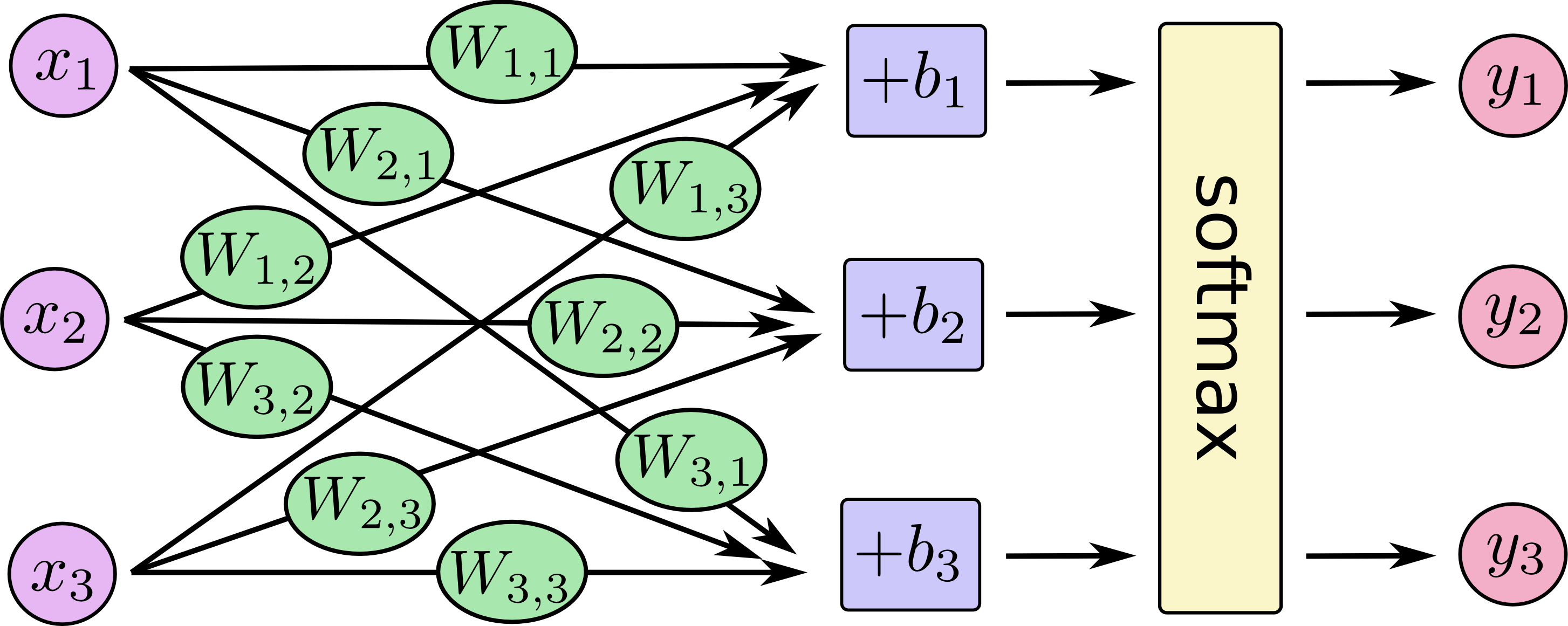
もし方程式にするのであれば、以下が得られます。
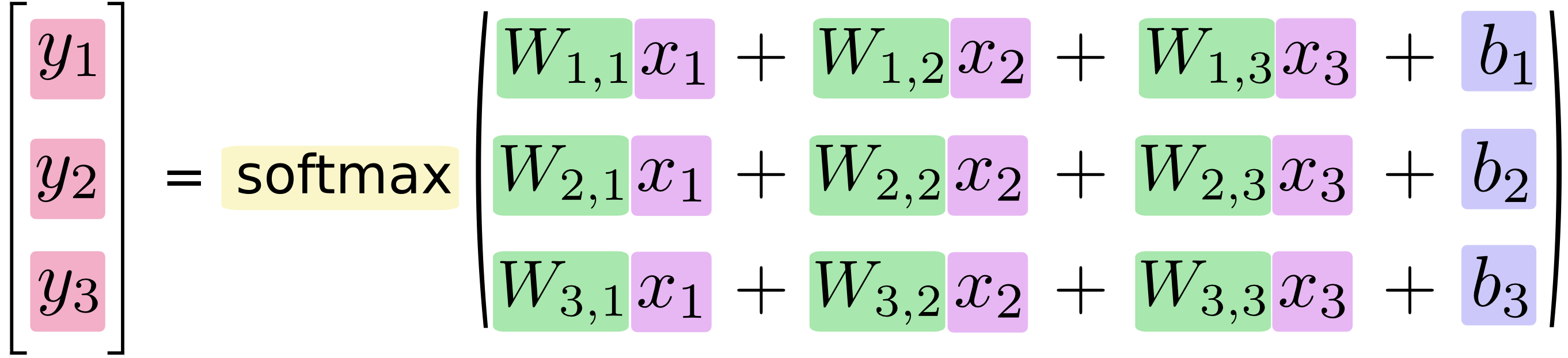
この手順をベクトル化して、行列の乗算に変換します。
これはコンピュータの能率に対して効果的です。(それは考え方にも有用です)
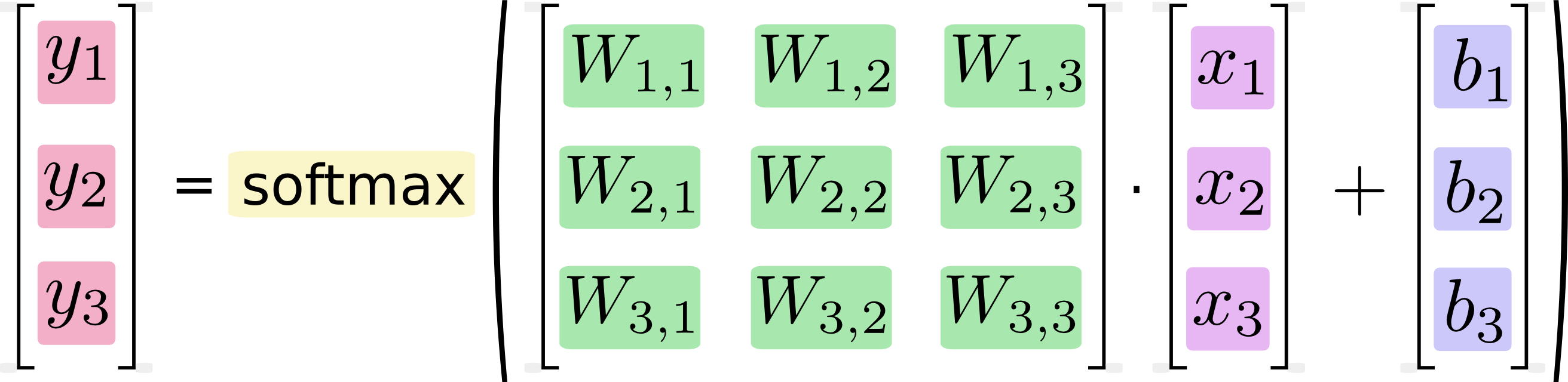
よりコンパクトに、以下のように単純に書くこともできます。
y = softmax(Wx + b)
回帰の実装
Pythonでの効率的な数値計算をするには、一般的にPython外の行列の乗算のような重い処理の演算をするNumPyのようなライブラリーを使い、他の言語に実装された効率のよいコードを使います。
残念ながら、Pythonの全ての演算に切り替えるのに多くのオーバーヘッドがあります。
このオーバーヘッドは、もしGPUで処理を実行するか、分散形式の場合にとりわけ悪く、データ転送に高いコストがかかります。
TensorFlowもまたpythonの外に重くありますが、しかしステップを踏むことでこのオーバーヘッドを避けることができます。
Pythonから独立した単一の重い演算の代わりに、TensorFlowは完全にPythonの外の相互の演算のグラフを描くことを可能にしています。
(このようなアプローチは、少ない機械学習のライブラリーに見られます)
TensorFlowを使うには、それをインポートする必要があります。
import tensorflow as tf
これらの相互演算を、記号変数を処理することで描きます。1つつくってみましょう。
x = tf.placeholder(tf.float32, [None, 784])
xは一定の値ではありません。
それはプレースホルダで、その値は計算を実行するためのTensorFlowへの問い合わせの際に入力します。
私達は、いくつもの入力したMNISTの画像を、それぞれ784次元のベクトルに平坦化したいです。
私達はこれを、[Noneg,784]の型の2Dの浮動小数のテンソルとして表します。
(次元は何の長さにもなりうるという意味ではありません)
私達もまた、モデル重みとバイアスを必要としています。
私達はこれらを追加の入力のように扱うことを想像できますが、TensorFlowはこれらでさえもよりよく扱う方法です:変数Aはインタラクティブな演算のTensorFlowのグラフに存在する変更可能なテンソルです。
それは使用可能で計算によって修正されました。
機械学習のアプリケーションにおいては、一般的に変数によってモデルのパラメーターを持ちます。
W = tf.Variable(tf.zeros([784, 10]))
b = tf.Variable(tf.zeros([10]))
私達は、変数の初期値のtf.Variableに与えることによってこれらの変数をつくります。
このケースでは、Wとbの両方をゼロで満たしたテンソルのように初期化します。
Wとbについて学ぶと、それらの初期値が何であるかがそれほど問題にならないでしょう。
Wは[784,10]の型ですなぜならそれの784次元画像のベクトルを、異なるクラス10次元のベクトル掛けたいです。
bは[10]の型を持っていて、出力に加えることができます。
ここまできて、モデルを満たすことができます。それは1つのラインを要します。
y = tf.nn.softmax(tf.matmul(x, W) + b)
最初に、xとWの乗算をtf.matmul(x, W)と表現します。
これは方程式においてそれらを掛けることで反転され、そこで複数の入力の2Dテンソルのxのように扱う小さなコツのようなWxを持ちます。
私達はそこでbを加え、そして最終的にtf.nn.softmaxを適用します。
それでおしまいです。
それはただ私達に、セットアップの短い線の組の後にモデルを定義するための1つの線を取ります。
それはTensorFlowがソフトマックス回帰をとりわけ簡単にするためいデザインされているからではありません。それは単に機械学習のモデルから物理シュミレーションからの幾通りの数値計算を描くための柔軟な方法です。
そしていったん定義されれば、モデルは異なるデバイスで動作できます。(コンピューターのCPUやGPU、そして携帯電話すら)
トレーニング
モデルをトレーニングするために、私達は良いモデルとは何を意味しているかの定義を必要とします。
実際には、機械学習において私達は一般的に、コストまたは損失を呼ぶののを悪いモデルと定義し、そしてどう悪いのかの最小化を試みます。しかしその2つは同じことです。
とても共通として、とてもよいコスト関数は「クロスエントロピー」です。
驚いたことに、クロスエントロピーは情報リオンにおける情報圧縮コードについて考えることから生じますが、しかしながらそれは多くのエリアにおける重要なアイデアを機械学習へのギャンブルに引き上げます。
それは定義されます。
Hy′(y)=−∑iyi′log(yi)
yは予測された確率分布であり、y’は真の分布(入力するであろうひとつの熱いベクトル)です。
いくつの大雑把な判断では、クロスエントロピーはどれだけ真を描くための予測に無駄が多いかを計測します。
クロスエントロピーのより多くの詳細は、このチュートリアルの範囲を超えていますが、しかしそれは理解する価値があります。
クロスエントロピーを実装するために最初に新しいプレースホルダーを正しい解に入力する必要があります。
y_ = tf.placeholder(tf.float32, [None, 10])
そこで私達はクロスエントロピー−∑y′log(y)を実装できます。
cross_entropy = tf.reduce_mean(-tf.reduce_sum(y_ * tf.log(y), reduction_indices=[1]))
最初に、tf.logはそれぞれの要素の対数を計算します。次に、tf.log(y)の要素の_yの要素を乗算します。
そしてtf.reduce_sumはreduction_indices=[1]のパラメータのため、yの2つ目の次元の中の要素に加えます。
最終的に、tf.reduce_meanはバッチの中のすべての例の中央値を計算します。
今は私達は、モデルが何をするべきかを知り、それは、訓練したTensorFlowを持つのにとても簡単です。
なぜならTensorFlowは計算のグラフ全体を知り、それは自動的にバックプロパゲーションアルゴリスム(誤差逆伝搬法)を、どう変数が最小化のコストに影響するかを効率的に決定するために自動的に使うことができます。
そこで選択した最適化のアルゴリズムを、変数を変更してコストを下げるために適用することができます。
train_step = tf.train.GradientDescentOptimizer(0.5).minimize(cross_entropy)
このケースでは、私達はTensorFlowに尋ねます 50%の傾斜の勾配降下アルゴリズムを使ってクロスエントロピーを最小化することは単純な手順で、そこでTensorFlowは単純にそれぞれの変数を少しのビットをそのコストを減少する方向に移動します。
しかしTensorFlowもまた多くの最適化アルゴリズムを提供します。(1つはラインを調整するだけのことです。)
TensowFlowが実際ここで何をするかは、場合により、新しい操作をバックプロパゲーション(誤差逆伝播法)と勾配降下を実装するグラフに加えます。
そこでそれは単一の操作を変換し、実行したとき、勾配降下の訓練のステップをし、変数をコストを下げるために微調整します。
これでモデルを訓練する準備ができました。
最後にはじめる前に、作成した変数を初期化する操作を加える必要があります。
init = tf.initialize_all_variables()
これで、セッションでモデルを開始することができ、そして変数を初期化する操作を実行できます。
sess = tf.Session()
sess.run(init)
さあ、訓練しましょう。1000回トレーニングのステップを実行します。
for i in range(1000):
batch_xs, batch_ys = mnist.train.next_batch(100)
sess.run(train_step, feed_dict={x: batch_xs, y_: batch_ys})
それぞれのループにおけるステップで、訓練のセットから100のランダムなデータのバッチを得ることができます。
プレースホルダーを置き換えるためにバッチデータの訓練のステップを実行します。
小さなランダムのデータのバッチを使うことを、確率論的な訓練と呼ばれています。
–このケースでは、確率論的勾配降下です。
理想的には、すべての訓練のステップですべてのデータを使いたい、なぜなら何をするべきかのよりよいセンスを提供してくれるからで、しかしそれは高価です。
そこで代わりに、異なる部分集合をいつも使います。
これを行うのは安くて同様の利益を持っています。
モデルを評価する
モデルはどうするでしょうか?
いいでしょう、最初に、どこで正しいラベルを予測するかを解いてみましょう。
tf.argmaxは極度に使いやすい関数で、それはいくつかの軸のテンソルの高いエントリーのインデックスを与えます。
例えば、tf.argmax(y,1)はモデルのラベルで、それぞれの入力に最も近く、tf.argmax(y_,1) が正しいラベルです。
私達はtf.equalを、予測が真とマッチする場合にチェックに使うことができます。
correct_prediction = tf.equal(tf.argmax(y,1), tf.argmax(y_,1))
これはブール数のリストを与えます。
何の部分が正しいかを特定するため、浮動小数をキャストし、中央値を取り出します。
例えば、[True, False, True, True]は[1,0,1,1] になり、0,75となります。
accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))
最終的に、テストデータに正確さを問い合わせます。
print(sess.run(accuracy, feed_dict={x: mnist.test.images, y_: mnist.test.labels}))
これはおよそ92%になるでしょう。
いかがでしょうか?
いや、そうでもないですよ。
実際に、それはとても悪いです。
これはとても簡単なモデルを使うからです。
小さな変更を伴うとき、97%を得ることがでいます。
最高のモデルであれば99.7%の正確さを超えることができます!(より多くの情報については、結果表を見て下さい。)
このモデルから学ぶことの何が問題でしょう。
まだ、これらの結果について少しがっかりすることがあるのであれば、より良くした次のチュートリアルを調べてみて、どうやってより洗練されたTensorFlowを使ったモデルを構築するかを学んでください。